- 포물선 운동에서 중간값 정리가 가지는 의미는 무엇일까?
- 포물선 운동이 이차곡선 형태라고 하는데, 포물선 운동을 이차곡선으로 표현하면 타원 궤도를 표현할 수 있지 않을까?
- 저항력은 상대운동으로 인해 생기는데, 만약 바람이 부는 방향으로 달리면 앞쪽에는 저항력이 생기지 않나?
- 유효 단면적에서 단면의 넓이를 사용하는 이유는 무엇일까? 구와 원을 비교해봤을 때 구가 더 많은 입자와 부딪힐 것 같은데, 그 양이 적어서 근사하는걸까? 아니면 물체가 빠르게 이동하기 때문에 입자들이 부딪히는 수에 거의 차이가 없다고 보는걸까?
- 부력과 항력의 차이는 무엇일까? 움직임에 의해 주변 공기의 압력이 변화면서 생기는 힘이 항력 아닐까?
- 도르래(베어링?)에 하중이 걸렸을 때 도르래와 축 사이의 마찰은 도르래가 변화 시키는 힘의 각도와 어떤 관련이 있을까? 만약 힘을 변화 시키는 각도와 도르래와 축 사이의 마찰의 관계가 선형이 아니라면 도르래의 개수에 따라 효율적인 배치가 있지 않을까?
- 상대 운동을 하는 관찰자는 인해 고정된 전하가 만들어내는 전기장을 자기장처럼 느낄 수 있을까?
- 도르래에서 줄이 미끄러지지 않고 버틸 수 있는 하중은 도르래의 배치, 개수와 관련이 있을까?
- 질문 동기: 크레인이나 승강기와 같이 물체를 들어 올릴 때 도르래를 많이 사용하는데, 어떻게 물체를 안정으로 들어 올리는 지 궁금하였고, 도르래의 배치에 따라 변할 수 있는지 궁금해서 찾아보게 되었다.
- 찾아보기 전 생각: 마찰은 도르래와 줄 사이의 수직 항력에 비례하기 때문에 도르래에서 줄을 당기는 힘과 각도가 같다면, 전체 도르래에서 미끄러지지 않고 버틸 수 있는 하중은 같을 것이다. 즉, 도르래 1개를 쓰든 2개를 쓰든 버틸 수 있는 하중에 차이가 없을 것이다.
- 해결 과정: 아래 그림과 같이 질량이 m, M인 물체가 도르래에서 장력의 평형을 이룬다고 할 때, 다음과 같은 식을 얻을 수 있다.
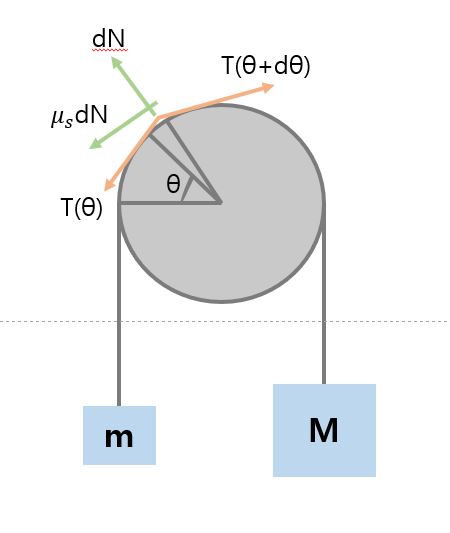 위 식을 연립하여 를 구할 수 있다.
위 식을 연립하여 를 구할 수 있다.
이러한 식을 캡스턴 방정식이라고 부른다. 이를 통해 도르래에서 줄이 미끄러지기 위해 필요한 힘을 구해보면 다음과 같다.
즉, 마찰력과 각도가 적당히 크다면 더 적은 힘으로도 물체를 지탱할 수 있다. 이를 통해 도르래를 1개만 사용하였을 때와 여러 개를 사용할 때를 생각해보면, 1개일 때는 위 식처럼 각도에 따라 지수함수 꼴로 나타날 것이고, 여러 개일 때는 각 도르래에서 가 변하는 것이므로 결국 마지막 도르래가 버틸 수 있는 하중은 로 1개일 때와 동일할 것이다. 처음 생각해보았던 것과 결과는 같지만 과정이 달랐다.
- 알게된 점: 도르래에서 마찰력은 각도에 대해 선형이 아니라 지수함수 꼴로 변화하며 이를 통해 당기는 힘보다 더 큰 하중을 견딜 수 있다. 또, 선박을 고정 시킬 때 이를 활용하여 줄을 여러 번 감아 적은 힘으로 고정시킬 수 있다.